3月20日

笔记

白化处理

相关理论

白化这个词，可能在深度学习领域比较常遇到，挺起来就是高大上的名词，然而其实白化是一个比PCA稍微高级一点的算法而已，所以如果熟悉PCA，那么其实会发现这是一个非常简单的算法。
白化的目的是去除输入数据的冗余信息。假设训练数据是图像，由于图像中相邻像素之间具有很强的相关性，所以用于训练时输入是冗余的；白化的目的就是降低输入的冗余性。

输入数据集X，经过白化处理后，新的数据X’满足两个性质：

1. 特征之间相关性较低；
2. 所有特征具有相同的方差。
   其实我们之前学的PCA算法中，可能PCA给我们的印象是一般用于降维操作。然而其实PCA如果不降维，而是仅仅使用PCA求出特征向量，然后把数据X映射到新的特征空间，这样的一个映射过程，其实就是满足了我们白化的第一个性质：除去特征之间的相关性。因此白化算法的实现过程，第一步操作就是PCA，求出新特征空间中X的新坐标，然后再对新的坐标进行方差归一化操作。

算法概述

白化分为PCA白化、ZCA白化

2.1 首先是PCA预处理

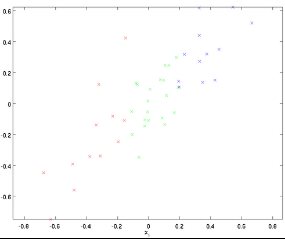
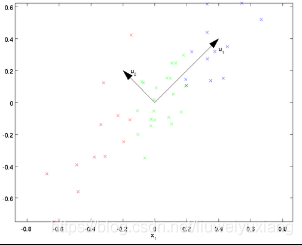
上面图片，左图表示原始数据X，然后我们通过协方差矩阵可以求得特征向量u1、u2，然后把每个数据点，投影到这两个新的特征向量，得到进行坐标如下：

这就是所谓的pca处理。

2.2 PCA白化

所谓的pca白化是指对上面的pca的新坐标X’,每一维的特征做一个标准差归一化处理。因为从上面我们看到在新的坐标空间中，(x1,x2)两个坐标轴方向的数据明显标准差不同，因此我们接着要对新的每一维坐标做一个标注差归一化处理：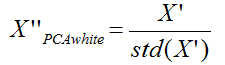

当然你也可以采用下面的公式：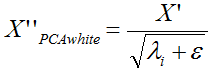

X’为经过PCA处理的新PCA坐标空间,然后λi就是第i维特征对应的特征值（前面pca得到的特征值），ε是为了避免除数为0。

2.3 ZCA白化

ZCA白化是在PCA白化的基础上，又进行处理的一个操作。具体的实现是把上面PCA白化的结果，又变换到原来坐标系下的坐标：给人的感觉就像是在PCA空间做了处理完后，然后又把它变换到原始的数据空间，使得变换后的数据更接近原始数据。

计算机视觉评价指标

图像分类

Top-1 error rate：将输出的C维向量按照降序排列，如果最大值所对应label与ground truth label不符，则该图片属于分类错误，最后用分类错误的样本数量除以样本集的数量得到Top-1 error rate；

Top-5 error rate：将输出的C维向量按照降序排列，如果前5个对应的label没有包含ground truth label，则该图片属于分类错误，最后用分类错误的样本数量除以样本集的数量得到Top-5 error rate；

目标检测

AP

AP，average precision，平均精确度，比上文precision多了一个average，显然计算AP时有一个求平均的过程。在上文precision和recall的介绍中，两者是存在一定关系的，当调整算法的阈值提高recall时，precision会降低，反之，precision会提高，通俗的说就是提高recall可以让检测出来的样本更多的预测为正样本（减少FN），但这样会让一些负样本也预测为正样本（FP增高），导致precision降低。通过多次调整阈值，可以获得不同recall下的precision，最后累加这些precision求平均便得到了average precision。

预测的bounding box和ground truth bounding box之间的关系用IoU表示，IoU（Intersection over Union，交并比），指的是预测的bounding box和ground truth bounding box之间的交集和并集的面积比值，当两者完全重合时，IoU为100%，没有任何交集时为0，显然IoU值越大，模型预测的bounding box性能越好。

Top-N ranked指的对排序后的样本统计数据按照前n个样本划分N次rank，分别求出每次rank后的precision和recall，直至n=N，N为预测的总数量。

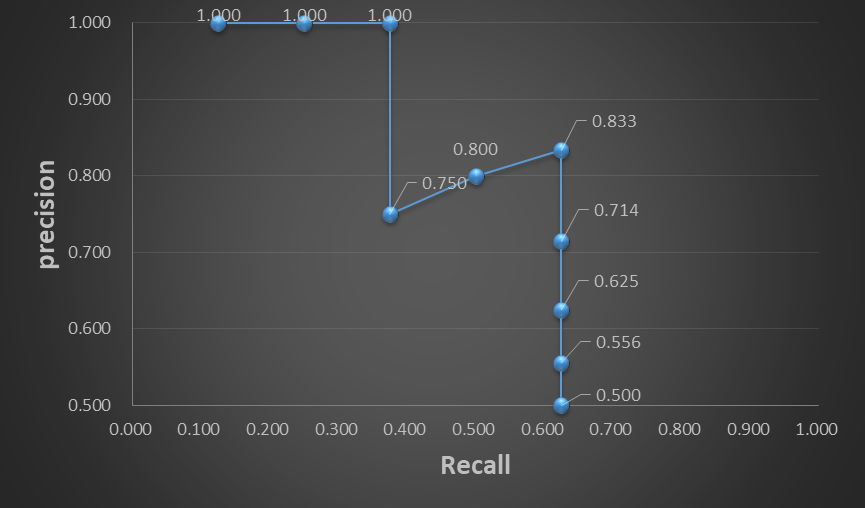
AP就是计算这条precision-recall曲线下的面积（area under curve，AUC）。

mAP

AP指的是一个类别的指标（如上文的狗检测例子），而一个object detection任务包含多个类别，如VOC包含20类object，则会计算出20个AP，将其累加取平均便得到mAP。

混淆矩阵

混淆矩阵又被称为错误矩阵， 在每个类别下，模型预测错误的结果数量，以及错误预测的类别和正确预测的数量都在一个矩阵下面显示出来，方便直观的评估模型分类的结果。